通信之美(1)：从频域看调制

这是拖延症的结果。。。

此为开篇第一篇，可是无论从那个角度来说这都不应该是第一篇。其实我是打算从高中数学讲起的，只是曾经想好的前两篇一直都不想写，然后因为某些原因这个是“必须”写的，所以为第一篇。

通信原理，其实就是数学公式推导，我知道大家都不喜欢数学公式，所以我就尽量避免数学公式，并且会在后面列出一些数学公式，免得想知道的人再去查书。

学习，重要的是时刻记得需要解决的问题，否则你只会看到书上用数学公式推导来推导去没什么意义。通信需要解决的问题就是，在发送端发送一个信号，在接收端恢复出这个信号。所以数学公式的推导就是，从一个函数开始，进行了好多的变换，最终的结果还是这个函数。如果你不知道要解决的问题是什么，那么你会发现，这么多数学推导没什么意义。所以最重要的就是，你要知道问题是什么。

调制，就是把低频信号变成高频信号的过程。至于为什么要调制，主要是为了让信号适合在信道上传输和防止不同路的信号相互干扰，具体的自己百度之。调制解调要解决的问题就是把低频信号变成相应的高频信号，然后再变回此低频信号的过程。请时刻记得调制解调要解决的这个问题，无论是什么调制方式。只不过不同的调制方式改进了原始的解决方案，于是就会遇到新的问题，不同的调制方式就是解决这些不同问题的。

既然是从要把低频信号变成高频信号，是不是从频域理解更容易懂一些？另外，有些人不能从潜意识上接受这个事实——从时域表示信号和从频域表示信号是没有区别的，就像五分之一和0.2的区别一样——我只能说多锻炼吧。

下面都是信号与系统中的基本公式。不记得的面壁思过去。

函数与冲击函数卷积的结果就是把函数平移：

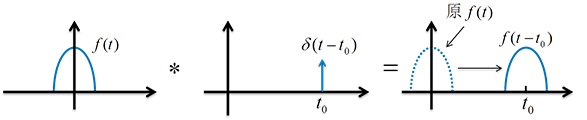
余弦函数\( cos(\omega_0t) \)的傅里叶变换是：

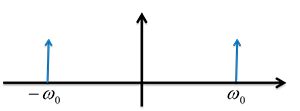
时域乘积到频域就是卷积。那么\( f(t)cos(\omega_0t) \)的傅里叶变换是(忽略前面的系数)：

好了，现在就已经把低频信号\( f(t) \)平移到了高频\( \omega_0t \)附近，这就是调制，就这么简单。

那么解调就是再平移回来:

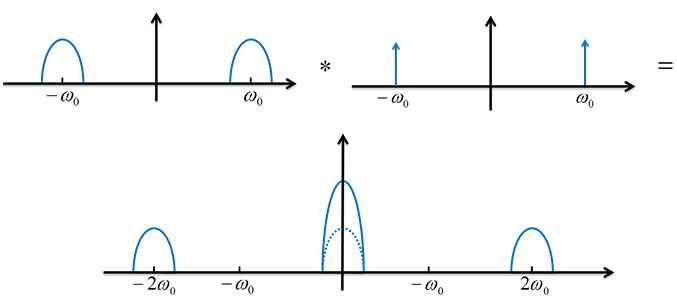
然后只取低频信号就是原始信号 \( f(t) \)了。所以通信系统就是：

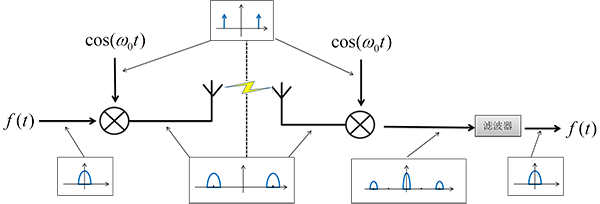
这就是最基本的调制系统，实际的实现就是在这个基础上的改进或是因为器件不理想添加了一些东西。对于早期的调制方式，比如AM、FM、PM、DSB、SSB等，因为没有成熟的数学理论所以在调制解调（主要是解调）方面的实现不是这样的。但是也是可以使用这种通用的调制解调方案的，所以说数学很重要。

有些时候滤波器会换成积分器，其实积分器就是低通滤波器，为什么呢？不(deng)告(dai)诉(geng)你(xin)。

下面是详细的数学公式，不想看的就不要看了。

函数与冲击函数的卷积： \begin{equation} f(t)\ast\delta(t-t_0)=f(t-t_0) \end{equation}

\( f(t)\ h(t)\ y(t) \)对应的傅里叶变换是 \( F(j\omega)\ H(j\omega)\ Y(j\omega) \)则有：

\begin{equation} y(t)=f(t)h(t)\Leftrightarrow{}Y(j\omega)=\frac{1}{2\pi}F(j\omega)\ast{}H(j\omega) \end{equation}

余弦函数 \( cos(\omega_0t) \)的傅里叶变换：

\begin{equation} \pi(\delta(\omega{}+\omega_0)+\delta(\omega-\omega_0)) \end{equation}